Alignment consistency
7.4. Alignment consistency#
Import Python libraries
from __future__ import annotations
import logging
import os
import cairosvg
import jax.numpy as jnp
import matplotlib.pyplot as plt
import sympy as sp
from numpy.testing import assert_almost_equal
from tensorwaves.data import SympyDataTransformer
from tqdm.auto import tqdm
from polarimetry.amplitude import AmplitudeModel, simplify_latex_rendering
from polarimetry.data import create_data_transformer, generate_meshgrid_sample
from polarimetry.io import (
display_latex,
mute_jax_warnings,
perform_cached_doit,
perform_cached_lambdify,
)
from polarimetry.lhcb import (
flip_production_coupling_signs,
load_model_builder,
load_model_parameters,
)
from polarimetry.lhcb.particle import load_particles
from polarimetry.plot import add_watermark, use_mpl_latex_fonts
mute_jax_warnings()
simplify_latex_rendering()
NO_TQDM = "EXECUTE_NB" in os.environ
if NO_TQDM:
logging.getLogger().setLevel(logging.ERROR)
model_choice = 0
model_file = "../../data/model-definitions.yaml"
particles = load_particles("../../data/particle-definitions.yaml")
amplitude_builder = load_model_builder(model_file, particles, model_choice)
imported_parameter_values = load_model_parameters(
model_file, amplitude_builder.decay, model_choice, particles
)
models = {}
for reference_subsystem in [1, 2, 3]:
models[reference_subsystem] = amplitude_builder.formulate(
reference_subsystem, cleanup_summations=True
)
models[reference_subsystem].parameter_defaults.update(imported_parameter_values)
models[2] = flip_production_coupling_signs(models[2], subsystem_names=["K", "L"])
models[3] = flip_production_coupling_signs(models[3], subsystem_names=["K", "D"])
Show code cell source
display_latex(m.intensity.cleanup() for m in models.values())
\[\begin{split}\displaystyle \begin{array}{c}
\sum_{\lambda_{0}=-1/2}^{1/2} \sum_{\lambda_{1}=-1/2}^{1/2}{\left|{\sum_{\lambda_0^{\prime}=-1/2}^{1/2} \sum_{\lambda_1^{\prime}=-1/2}^{1/2}{A^{1}_{\lambda_0^{\prime}, \lambda_1^{\prime}, 0, 0} d^{\frac{1}{2}}_{\lambda_1^{\prime},\lambda_{1}}\left(\zeta^1_{1(1)}\right) d^{\frac{1}{2}}_{\lambda_{0},\lambda_0^{\prime}}\left(\zeta^0_{1(1)}\right) + A^{2}_{\lambda_0^{\prime}, \lambda_1^{\prime}, 0, 0} d^{\frac{1}{2}}_{\lambda_1^{\prime},\lambda_{1}}\left(\zeta^1_{2(1)}\right) d^{\frac{1}{2}}_{\lambda_{0},\lambda_0^{\prime}}\left(\zeta^0_{2(1)}\right) + A^{3}_{\lambda_0^{\prime}, \lambda_1^{\prime}, 0, 0} d^{\frac{1}{2}}_{\lambda_1^{\prime},\lambda_{1}}\left(\zeta^1_{3(1)}\right) d^{\frac{1}{2}}_{\lambda_{0},\lambda_0^{\prime}}\left(\zeta^0_{3(1)}\right)}}\right|^{2}} \\
\sum_{\lambda_{0}=-1/2}^{1/2} \sum_{\lambda_{1}=-1/2}^{1/2}{\left|{\sum_{\lambda_0^{\prime}=-1/2}^{1/2} \sum_{\lambda_1^{\prime}=-1/2}^{1/2}{A^{1}_{\lambda_0^{\prime}, \lambda_1^{\prime}, 0, 0} d^{\frac{1}{2}}_{\lambda_1^{\prime},\lambda_{1}}\left(\zeta^1_{1(2)}\right) d^{\frac{1}{2}}_{\lambda_{0},\lambda_0^{\prime}}\left(\zeta^0_{1(2)}\right) + A^{2}_{\lambda_0^{\prime}, \lambda_1^{\prime}, 0, 0} d^{\frac{1}{2}}_{\lambda_1^{\prime},\lambda_{1}}\left(\zeta^1_{2(2)}\right) d^{\frac{1}{2}}_{\lambda_{0},\lambda_0^{\prime}}\left(\zeta^0_{2(2)}\right) + A^{3}_{\lambda_0^{\prime}, \lambda_1^{\prime}, 0, 0} d^{\frac{1}{2}}_{\lambda_1^{\prime},\lambda_{1}}\left(\zeta^1_{3(2)}\right) d^{\frac{1}{2}}_{\lambda_{0},\lambda_0^{\prime}}\left(\zeta^0_{3(2)}\right)}}\right|^{2}} \\
\sum_{\lambda_{0}=-1/2}^{1/2} \sum_{\lambda_{1}=-1/2}^{1/2}{\left|{\sum_{\lambda_0^{\prime}=-1/2}^{1/2} \sum_{\lambda_1^{\prime}=-1/2}^{1/2}{A^{1}_{\lambda_0^{\prime}, \lambda_1^{\prime}, 0, 0} d^{\frac{1}{2}}_{\lambda_1^{\prime},\lambda_{1}}\left(\zeta^1_{1(3)}\right) d^{\frac{1}{2}}_{\lambda_{0},\lambda_0^{\prime}}\left(\zeta^0_{1(3)}\right) + A^{2}_{\lambda_0^{\prime}, \lambda_1^{\prime}, 0, 0} d^{\frac{1}{2}}_{\lambda_1^{\prime},\lambda_{1}}\left(\zeta^1_{2(3)}\right) d^{\frac{1}{2}}_{\lambda_{0},\lambda_0^{\prime}}\left(\zeta^0_{2(3)}\right) + A^{3}_{\lambda_0^{\prime}, \lambda_1^{\prime}, 0, 0} d^{\frac{1}{2}}_{\lambda_1^{\prime},\lambda_{1}}\left(\zeta^1_{3(3)}\right) d^{\frac{1}{2}}_{\lambda_{0},\lambda_0^{\prime}}\left(\zeta^0_{3(3)}\right)}}\right|^{2}} \\
\end{array}\end{split}\]
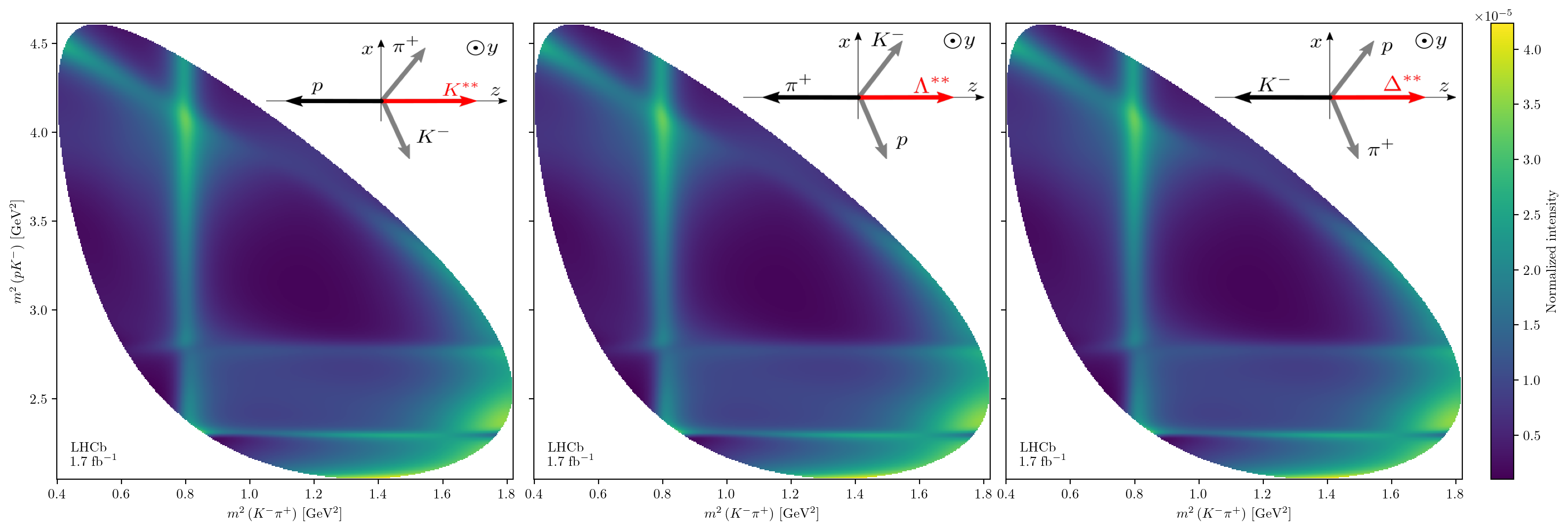
See DPD angles for the definition of each \(\zeta^i_{j(k)}\).
Note that a change in reference sub-system requires the production couplings for certain sub-systems to flip sign:
Sub-system 2 as reference system: flip signs of \(\mathcal{H}^\mathrm{production}_{K^{**}}\) and \(\mathcal{H}^\mathrm{production}_{L^{**}}\)
Sub-system 3 as reference system: flip signs of \(\mathcal{H}^\mathrm{production}_{K^{**}}\) and \(\mathcal{H}^\mathrm{production}_{D^{**}}\)
unfolded_intensity_exprs = {
reference_subsystem: perform_cached_doit(model.full_expression)
for reference_subsystem, model in tqdm(models.items(), disable=NO_TQDM)
}
subs_intensity_exprs = {
reference_subsystem: expr.xreplace(
models[reference_subsystem].parameter_defaults
)
for reference_subsystem, expr in unfolded_intensity_exprs.items()
}
intensity_funcs = {
reference_subsystem: perform_cached_lambdify(expr, backend="jax")
for reference_subsystem, expr in tqdm(
subs_intensity_exprs.items(), disable=NO_TQDM
)
}
transformer = {}
for reference_subsystem in tqdm([1, 2, 3], disable=NO_TQDM):
model = models[reference_subsystem]
transformer.update(create_data_transformer(model).functions)
transformer = SympyDataTransformer(transformer)
grid_sample = generate_meshgrid_sample(model.decay, resolution=400)
grid_sample = transformer(grid_sample)
intensity_grids = {i: func(grid_sample) for i, func in intensity_funcs.items()}
Show code cell source
{i: jnp.nansum(grid) for i, grid in intensity_grids.items()}
{1: Array(3.91663029e+08, dtype=float64),
2: Array(3.91663029e+08, dtype=float64),
3: Array(3.91663029e+08, dtype=float64)}
assert_almost_equal(
jnp.nansum(intensity_grids[2] - intensity_grids[1]), 0, decimal=6
)
assert_almost_equal(
jnp.nansum(intensity_grids[2] - intensity_grids[1]), 0, decimal=6
)
Show code cell source
def convert_svg_to_png(input_file: str, dpi: int) -> None:
output_file = input_file.replace(".svg", ".png").replace(".SVG", ".png")
with open(input_file) as f:
src = f.read()
cairosvg.svg2png(bytestring=src, write_to=output_file, dpi=dpi)
def overlay_inset(
png_file: str, ax, position: tuple[float, float], width: float
) -> None:
image = plt.imread(png_file)
res_x, res_y, _ = image.shape
x_min, x_max = ax.get_xlim()
y_min, y_max = ax.get_ylim()
aspect_ratio = res_x / res_y
aspect_ratio /= (x_max - x_min) / (y_max - y_min)
extent = [
position[0],
position[0] + width,
position[1],
position[1] + width / aspect_ratio,
]
ax.imshow(image, aspect="auto", extent=extent, zorder=2)
ax.set_xlim(x_min, x_max)
ax.set_ylim(y_min, y_max)
for subsystem in ["K", "D", "L"]:
convert_svg_to_png(f"../_images/orientation-{subsystem}.svg", dpi=200)
del subsystem
def plot_comparison(use_watermark: bool) -> None:
plt.ioff()
x_label = R"$m^2\left(K^-\pi^+\right)$ [GeV$^2$]"
y_label = R"$m^2\left(pK^-\right)$ [GeV$^2$]"
plt.rcdefaults()
use_mpl_latex_fonts()
fig, axes = plt.subplots(
dpi=200,
figsize=(20, 6),
ncols=3,
sharey=True,
gridspec_kw={"width_ratios": [1, 1, 1.21]},
)
normalized_intensities = {
i: I / jnp.nansum(I) for i, I in intensity_grids.items()
}
global_max = max(map(jnp.nanmax, normalized_intensities.values()))
axes[0].set_ylabel(y_label)
subsystem_names = ["K", "L", "D"]
for i, (ax, name) in enumerate(zip(axes, subsystem_names), 1):
ax.set_xlabel(x_label)
ax.set_box_aspect(1)
mesh = ax.pcolormesh(
grid_sample["sigma1"],
grid_sample["sigma2"],
normalized_intensities[i],
)
mesh.set_clim(vmax=global_max)
if ax is axes[-1]:
c_bar = fig.colorbar(mesh, ax=ax)
c_bar.ax.set_ylabel("Normalized intensity")
if use_watermark:
add_watermark(ax)
overlay_inset(
f"../_images/orientation-{name}.png",
ax=ax,
position=(1.05, 3.85),
width=0.75,
)
fig.subplots_adjust(wspace=0)
output_filename = "intensity-alignment-consistency"
if use_watermark:
output_filename += "-watermark"
fig.savefig(f"../_static/images/{output_filename}.png", bbox_inches="tight")
if use_watermark:
plt.show()
plt.close(fig)
plt.ion()
plt.rc("font", size=18)
plot_comparison(use_watermark=False)
plot_comparison(use_watermark=True)